omgsoli.blogg.se - Loop the loop physics calculator

#Loop the loop physics calculator free

What do you THINK will happen when you release the ball at the upper line? What happens when you release the ball at the lower line?Īnswer: The ball doesn’t make it around the loop.

Put the ball on the track at a height h above the table (lower line on the track).

There are two lines on the track for the Loop the Loop, one at a height h (which is twice the radius, r, of the loop) and the other at the larger height H.

Kinetic energy (KE)is the energy the object has due to its motion.Ĭonservation of energy states that the total energy of a system remains constant, though it can change forms.

Potential energy (PE) is the energy the object has due to its position.

Work (W) is the energy given to the object by applying a force over a distance.

The three types of energy that we will be considering are: Work, Potential Energy, and Kinetic Energy. ΔU = (1.45 A.m 2)(0.The loop the loop is an example of conservation of energy. The change in potential energy of the coil when it is rotated 180 0 so that its magnetic moment is parallel to the field given by What is the change in potential energy of the coil when it is rotated 180 0 so that its magnetic moment is parallel to the field? (c) For Figure 5d, φ = 180 0, τ = NIAB sin 180 0 = 0, no direction and U = – μB cos 180 0 = NIABĪ coil with magnetic moment 1.45 A.m 2 is oriented initially with its magnetic moment antiparallel to a uniform 0.835 T magnetic field. (b) For Figure 5b, φ = 0 0, τ = NIAB sin 0 0 = 0, no direction and U = – μB cos 0 0 = – NIAB The magnitude of τ is equal to the magnitude of μ x B or τ = μ x B, and we can conclude immediately that the corresponding potential energy is U = – μB cos φ, where μ = NIB, τ = μB sin φ.

$loop the loop physics calculator$

Calculate the magnitude and direction of the torque τ and the value of the potential energy U as given in U = – μ x B= – μB cos φ, when the coil is oriented as shown in parts (a) through (d) of Fig. There is a uniform magnetic field B in the positive y-direction.

#Loop the loop physics calculator free

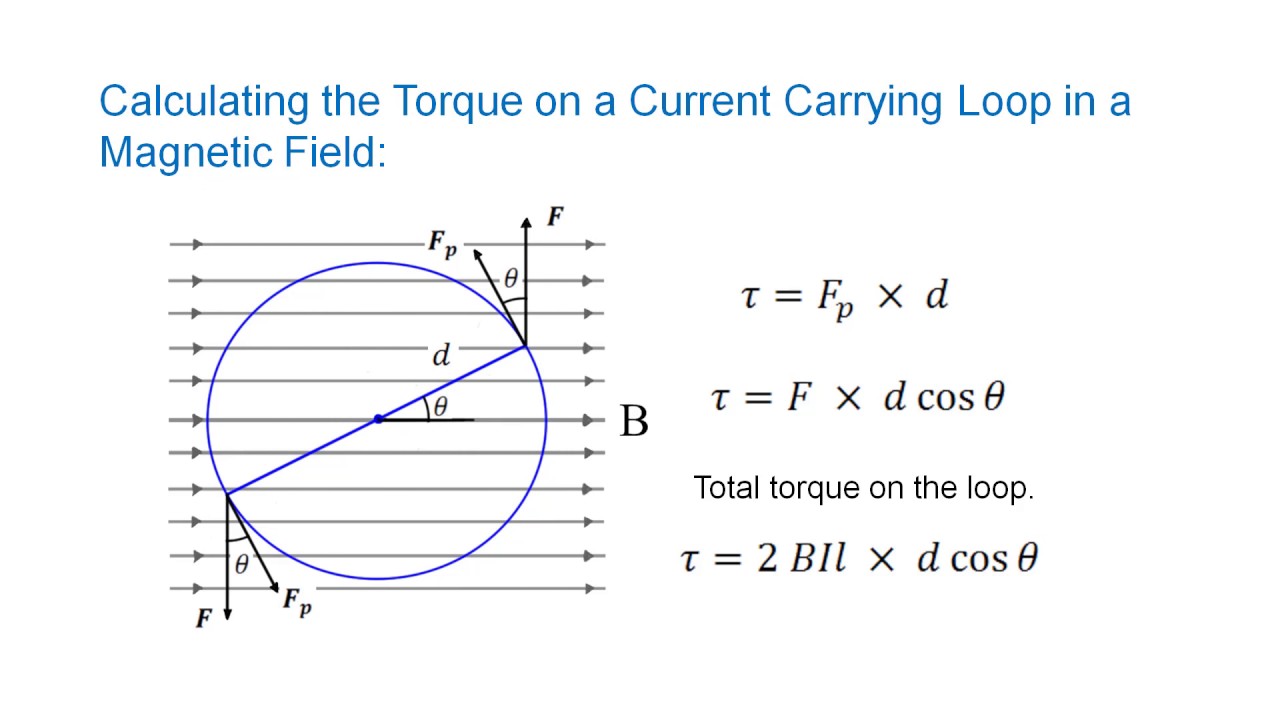
Α = ∑τ/I = 3.00 N.m/0.01031 kg.m 2 = 290.98 rad/s 2Ī circular coil with area A and N turns is free to rotate about a diameter that coincides with the x-axis. The 2 0.5-m sides rotate about their centers, and the 2 1.0-m sides rotate about a parallel axis. To find the moment of inertia of the coil, consider each side as a uniform bar. And each 0.500-m side has a mass of 0.0353 kg. Now, each 1.00 m side has a mass of 0.0707 kg. (b) the initial angular acceleration of the coil just after the current is started is Since t = IBA sin f then only the top and bottom sides will experience torque, thus will rotate about A 2. (a) About which axis (A 1 or A 2) will the coil begin to rotate? Why? (a) diagram showing the direction of the force that the magnetic field exerts on each segment of the circuit (ab, bc, etc.) shown by the Figure 2. (c) Use your results from part (b) to calculate the torque that the magnetic field exerts on the circuit about the hinge axis ab.Īrea, A = 20.0 cm x 35.0 cm = 0.2 m x 0.35 m Then calculate only those forces that exert this torque. (b) Of the four forces you drew in part (a), decide which ones exert a torque about the hinge ab. (a) Draw a clear diagram showing the direction of the force that the magnetic field exerts on each segment of the circuit (ab, bc, etc.). It carries a clockwise 5.00-A current and is located in a uniform 1.20-T magnetic field oriented perpendicular to two of its sides, as shown. The 20.0 cm x 35.0 cm rectangular circuit shown in Fig. (c) the maximum torque that can be obtained with the same total length of wire carrying the same current in this magnetic field is when maximum area is when the loop is circular with radiusĪ = πR 2 = π(0.0414 m) 2 = 5.38 x 10 -3 m 2 and (a) What torque acts on the loop? (b) What is the magnetic moment of the loop? (c) What is the maximum torque that can be obtained with the same total length of wire carrying the same current in this magnetic field?Īrea, A = 5.0 cm x 8.0 cm = 0.05 m x 0.08 m Problem#1The plane of a 5.0 cm x 8.0 cm rectangular loop of wire is parallel to a 0.19-T magnetic field.